Multi-view Learning with CCA based Approaches (Theory, Applications and Implementations)

Introduction

In real-world environments, the perception acquired with two or more sensory inputs are often correlated. For example consider a scenario where you are listening to a presentation, sensory systems for vision and hearing are constantly bombarded with visual and audio information which are often consensus and complimentary to each other.

In today’s applications, we often see an increase in availability of such sources which satisfies consensus and complimentary principles [1] to provide multiple views about the content. Figure-1 shows some such examples with 2 parallel views from diverse areas.

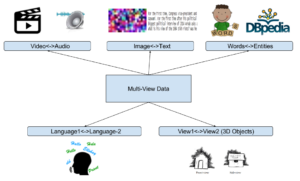
**Figure-1:** Example sources for Multi-view data **[Video<->Audio]** Image frames aligned with audio **[Image<->Text]** Text and Images observed together in Webpages, Wikipedia articles, Tweets **[Words<->Entities]** A word in the linguistic context and as an entity representing a real-world concept **[Language1<->Language2]** view of a topic in different languages **[View1<->View2]** Different viewpoints of 3D objects.

It can be beneficial to leverage these multiple views instead of a single-view for data driven learning. But directly adapting multiple views to the existing machine learning algorithms such as support vector machines etc., can only naively concatenate multiple views into a one single view for adapting to a learning setting. Also concatenation provide meaningless representation, as each independent view has its own specific property. This drawback has spawn interest in conducting Multi-View learning [2].

In contrast to the single view setting, Multi-view learning introduces one function to jointly optimize and exploit all views of the input data as different independent feature sets which can inherently help in learning a task with additional information. Given such possibilities, approaches [3] are formulated to use multi-view data for maximizing consensus. In general, a high consensus of two independent hypothesis are considered to result in a low generalization error. This makes Multi-view learning effective, more promising, and has better generalization ability than the single-view learning.

Several different formulations also emerged in the direction of Multi-view learning. If the labels of a view is acquired from the another view, then those labels are used for weak or self-supervision [4]. Similarly, large unlabeled data (i.e. unseen view) was leveraged for the supervised (i.e. seen view) classification tasks for self-taught learning [5] to transfer knowledge from unlabeled data. However, most of these areas also emerged themselves into different learning areas supporting various applications in many domains.

Progress in deep neural networks has also shown impact in Multi-view learning approaches (which will be covered in one of the upcoming articles). However in the following, this article aims to comprehend advantages and limitations of a multi-view learning method that was successfully applied over the past several years without deep architectures.

Learning with CCA and its Variations

Several CCA based approaches are proposed over the last two decades to support multi-view learning. CCA and its variations are considered as an approach for early fusion where the goal is to combine features extracted from individual views into a common representation. CCA is also seen as co-regularization method using complex information for feature selection for identifying better underling semantics. Subspace learning approaches [6] fall into this category and aim to obtain a latent subspace shared by multiple views. Advantage of such methods is to effectively eliminated the curse of dimensionality problem. In the following, detailed descriptions about popular CCA based variations that leveraged 2 or more views are presented.

Canonical Correlation Analysis (CCA)

Originally proposed by Hotelling [7], it aims to work on two views for finding the linear transformations of each single view such that the correlations between the transformed variables are maximized. Lets consider a two view data $\{X,Y\} = \{(x_1,y_1),....,(x_n,y_n)\}$ where $X \in \mathcal{R}^{d_1 \times n}, Y \in \mathcal{R}^{d_2 \times n}$ . Then CCA aims to compute two linear projections $w_x,w_y$ which makes the individual instances in $X,Y$ maximally correlated in the projected space and evaluated using the following correlation coefficient $\rho$ .

$\rho = \frac{w_{x}^TC_{xy}w_y}{\sqrt{(w_{x}^TC_{xx}w_x)(w_{y}^TC_{yy}w_y)}}$

where $C_{xy}$ is a cross-covariance matrix given as.

$C_{xy} = \frac{1}{n}\sum_{i=1}^{n}(x_i-\mu_x)(y_i-\mu_y)$

Here, $\mu_x,\mu_y$ represent means of two views $X,Y$ and $C_{xx}, C_{yy}$ are covariance matrices.

Maximizing linear projections $w_x,w_y$ of CCA is equivalent to solving a pair of generalized eigenvalue problems [8] and optimization is posed as a Lagrangian dual [9]. So finally, correlation between different views is provided by the eigenvector corresponding to the largest eigenvalues.

Besides successful application of CCA for having linear projections, there is still a need for introduction of non-linearity into linear methods.

Kernel Canonical Correlation Analysis (kCCA)

The kCCA [10] provides a non-linear extension of CCA. If we formalize kCCA in line with CCA, then dual representation is leveraged for representing $w_x,w_y$ by $X\alpha, Y\beta$ where $\alpha$ and $\beta$ are vectors of size n. So the correlation coefficient $\rho$ is provided by

$\rho = \frac{\alpha^{T}X^{T}XY^{T}Y\beta}{\sqrt{\alpha^{T}X^{T}XX^{T}X\alpha \times \beta^{T}Y^{T}YY^{T}Y\beta}}$

If kernel matrices $K_x,K_y$ of $X,Y$ is provided by $X^TX,Y^TY$ respectively. Then the earlier equation is rewritten as follows:

$\rho = \frac{\alpha^{T}K_xK_y\beta}{\sqrt{\alpha^{T}K_x^{2}\alpha \times \beta^{T}K_y^{2}\beta}}$

For maximizing linear projections, in contrast to the linear CCA which works by carrying out an eigen-decomposition of the covariance matrix. The eigenvalue problem for KCCA is degenerate solutions when either $K_x$ or $K_y$ is invertible [8].

Cluster Canonical Correlation Analysis (cluster CCA)

Before clustering, multiple views of the data are projected into lower dimensional subspace using CCA [11]. Given a two view data $\{X,Y\} = \{(x_1,y_1),....,(x_n,y_n)\}$ where $X \in \mathcal{R}^{d_1 \times n}, Y \in \mathcal{R}^{d_2 \times n}$ , Chaudhuri et al. [11] assumes that the each view is generated from mixture of Gaussian’s. Also, they assume views are uncorrelated. To ensure a sufficient correlation between views, CCA matrix across the views assumed to be at least $k-1$ , when each view is in isotropic position and the $(k-1)^{th}$ singular value of this matrix to be at least minimum eigen value. Now the correlation coefficient $\rho$ is provided by

$\rho = \frac{\mathbf{E}[(u.X) (v.Y)]}{\sqrt{\mathbf{E}[(u.X)^2]\mathbf{E}[(v.Y)^2]}}$

where $u,v$ are the projection vectors. In the dual formation, minimizing the equation provide the minimum eigen value satisfying the aforementioned conditions.

CCA was also combined with other clustering algorithms such as spectral clustering [12,13]. Also, other variations of cluster-CCA [14] exists which learn discriminant low dimensional representations that maximize the correlation between the two sets.

Sparse Canonical Correlation Analysis (sparse CCA)

The sparse CCA is formed as a sub selection procedure that reduces the dimensionality of the vectors to attain a stable solution [15]. Sparse CCA also aims to compute pair of linear projections $w_x,w_y$ that maximize the correlation coefficient $\rho$ provided by

$\rho = \frac{w_{x}^TC_{xy}w_y}{\sqrt{(w_{x}^TC_{xx}w_x)(w_{y}^TC_{yy}w_y)}}$

Even though, the Equation is similar to CCA. However, the constraints for sparse CCA [16] are different from those CCA and is provided by

$s.t. ||w_x||^2 \leq 1, ||w_y||^2 \leq 1, P_x(w_x) \leq c_x , P_y(w_y) \leq c_y$

where $P_x$ and $P_y$ are convex penalty functions. Advantage of sparse CCA criterion is that it results in unique $w_x$ and $w_y$ even when dimensions of each instance in $X$ and $Y$ are greater than total sample size for certain choice of $P_x$ and $P_y$ .

Probabilistic Canonical Correlation Analysis (probabilistic CCA)

In CCA, the canonical correlation directions given by $w_x$ and $w_y$ are obtained by solving generalized eigenvalue problem. However, making a latent variable interpretation and building a model to get maximum likelihood estimation (MLE) also leads to the canonical correlation directions [17]. Given latent variables $z, x$ and $y$ , then Gaussian prior and conditional distribution is given by

$z \sim \mathcal{N}(0,I_d)$

$x|z \sim \mathcal{N}(w_xz+\mu_{x},\Theta_x)$

$y|z \sim \mathcal{N}(w_yz+\mu_{y},\Theta_y)$

Now, the projection matrices $w_x,w_y$ estimated with MLE is given by

$w_x = \sum_{xx}U_xP^{1/2}R$

$w_y = \sum_{yy}U_yP^{1/2}R$

where $P$ is a diagonal matrix constituting canonical correlations, $R$ is an arbitrary rotation matrix and $U$ has canonical directions.

Other variations of probabilistic CCA also exist, where the Gaussian distributions replaced with Student-t distributions [18], hierarchical Bayesian model used with variational approximation [19] and learning from noisy data with variational Bayesian inference [20].

Regularized Canonical Correlation Analysis (regularized CCA)

Regularization can be seen as a way to deal with overfitting and help to generalize better for the unseen samples. Now if CCA seen from the perspective of an estimator of a linear system [21] underlying the data $X$ and $Y$ . Then regularized CCA aims to compute two normalized linear projections $w_x,w_y$ which makes the individual instances in $X,Y$ maximally correlated in the projected space and evaluated using the following correlation coefficient $\rho$ and optimized with maximum likelihood estimator.

$\rho = \frac{w_{x}^TC_{xy}w_y}{\sqrt{(w_{x}^TC_{xx}w_x+\tau_x||w_x||^{2})(w_{y}^TC_{yy}w_y+\tau_y||w_y||^{2})}}$

where $\tau_x,\tau_y$ are the regularization parameters and are bounded between interval [0,1] . Regularized CCA is also extended with kernel variations [22].

$\rho = \frac{w_{x}^TK_xK_yw_y}{\sqrt{(w_{x}^T(K_x+\tau_xI)^2w_{x})(w_{y}^T(K_y+\tau_yI)^2w_{y})}}$

Theoretical analysis is performed with regularized kernel CCA versions to investigate rates of regularization parameter [23].

Generalized Canonical Correlation Analysis (gCCA)

Aforementioned methods only leverage 2 views of the data, extending it to multiple views is achieved with generalized version of CCA [39]. In general, it is accomplished by combining all the pairwise correlations among each view through addition operation in the objective function [40]. If we consider a three view data $\{X,Y,Z\} = \{(x_1,y_1,z_1),....,(x_n,y_n,z_n)\}$ where $X \in \mathcal{R}^{d_1 \times n}, Y \in \mathcal{R}^{d_2 \times n}$ and $Z \in \mathcal{R}^{d_3 \times n}$ . Then gCCA aims to compute linear projections $w_x,w_y,w_z$ which makes the individual instances in $X,Y,Z$ maximally correlated in the projected space and evaluated using the following correlation coefficient $\rho$ .

$\rho = \frac{w_{x}^TC_{xy}w_y}{\sqrt{(w_{x}^TC_{xx}w_x)(w_{y}^TC_{yy}w_y)}} +\frac{w_{y}^TC_{yz}w_z}{\sqrt{(w_{y}^TC_{yy}w_z)(w_{z}^TC_{zz}w_z)}} +\frac{w_{x}^TC_{xz}w_z}{\sqrt{(w_{x}^TC_{xx}w_x)(w_{z}^TC_{zz}w_z)}}$

Now, Maximizing linear projections $w_x,w_y,w_z$ is equivalent that of two view CCA . Thus making CCA a merely the subset of gCCA [41]. Also, there exists the regularized version of gCCA [42].

Applications

Several applications from different disciplines have leveraged Multi-view learning with CCA based approaches for supervised or semi-supervised (classification, regression) and unsupervised (retrieval) tasks. Popular applications can be found in some of the applied areas of machine learning such as computer vision, natural language processing and multimedia information retrieval. In the following, we see some of the prominent applications from these areas.

Computer Vision Applications

Many problems in computer vision have leveraged single modality with multiple views for Multi-view learning with CCA based approaches. To name a few, 3D face reconstruction [24] is accomplished by identifying correlated linear features with the views emerging from depth and color of the images. Similarly, facial expression recognition [25] is attained by finding correlations between labeled graph vector and the semantic expression vector extracted from facial images. Reconstructing of a high resolution face image from one or more low resolution face images [26] also achieved by maximizing the correlation between the local neighbor relationships of high and low resolution images. Extension of basic CCA to tensors [27] provided a solution for identifying human action and gesture classification in videos. Combining CCA with locality methods such as locally linear embedding (LLE) and locality preserving projections (LPP) has shown applications to pose estimation [28]. Mapping 2D and 3D images is achieved by taking each view and learning a subspace with CCA regression [29].

There are also many other recent applications such as gait recognition, facial behavior analysis, human body shape estimation etc., which also leveraged CCA based methods.

Natural Language Processing Applications

One of the strong application of Multi-view learning based CCA methods for natural language processing is creation of distributed word representations either monolingual [30] or cross-lingual [31]. Also, CCA based methods were used for domain adaptation [32], and are proven closer to structural correspondence learning. POS tagging in low resource languages [33], similarity calculations between sentences across languages [34] and transliteration across languages [35] is achieved by leveraging parallel views across characters are few more applications.

Multimedia Information Retrieval

In multimedia information retrieval, multiple views are generally acquired from different modalities such as images, videos, speech and text. Here, Multi-view learning can also be comprehended as multimodal learning [36]. In particular when we observe the usage of CCA based methods in multimedia information retrieval, most of them belong to cross-modal retrieval [37] or hashing [38].

Implementations

Most of the major platforms that provide machine learning functionality support CCA based methods. Nevertheless in the following, different implementations using varied programming languages is presented.

MATLAB: CCA, kCCA, sparse CCA, probabilistic CCA, generalized CCA

R: CCA, kCCA, sparse CCA, generalized CCA

Python: CCA and gCCA, regularized kernel CCA

Conclusion

To conclude, Multi-view learning methods are built from the principles where learning using multiple views is expected to improve the generalization performance. Also, it is known as a data fusion approach from multiple sources or modalities. CCA based methods have been the core part of progress made in Multi-view learning approaches and is also expected to play an important role in theoretical and application advances in future when combined with recent deep and representation learning approaches for Multi-view learning.

References

[1] Xu, Chang, Dacheng Tao, and Chao Xu. A survey on multi-view learning. arXiv preprint arXiv:1304.5634 (2013).

[2] Virginia R. de Sa. Minimizing disagreement for self-supervised classification. In Proc. Connectionist Models Summer School (1994).

[3] Rüping, S. and Scheffer, T. Learning with multiple views. In Proc. ICML Workshop on Learning with Multiple Views (2005).

[4] Virginia R. de Sa. Learning classification with unlabeled data. In Advances in neural information processing systems (1994).

[5] Raina, R., Battle, A., Lee, H., Packer, B. and Ng, A.Y. Self-taught learning: transfer learning from unlabeled data. In Proc. ICML (2007).

[6] Fu, Y., Cao, L., Guo, G. and Huang, T.S. Multiple feature fusion by subspace learning. In Proc. international conference on Content-based image and video retrieval (2008).

[7] Hotelling, H. Relations between two sets of variates. Biometrika (1936).

[8] Hardoon, D.R., Szedmak, S. and Shawe-Taylor, J. Canonical correlation analysis: An overview with application to learning methods. Neural computation (2004).

[9] Sun, S. A survey of multi-view machine learning. Neural Computing and Applications (2013).

[10] Akaho, S. A kernel method for canonical correlation analysis. arXiv preprint cs/0609071 (2006).

[11] Chaudhuri, K., Kakade, S.M., Livescu, K. and Sridharan, K. Multi-view clustering via canonical correlation analysis. In Proc. international conference on machine learning (2009).

[12] Blaschko, M.B. and Lampert, C.H. Correlational spectral clustering. In Computer Vision and Pattern Recognition (2008).

[13] Kumar, A., Rai, P. and Daume, H. Co-regularized multi-view spectral clustering. In Advances in neural information processing systems (2011).

[14] Rasiwasia, N., Mahajan, D., Mahadevan, V. and Aggarwal, G. Cluster canonical correlation analysis. In Artificial Intelligence and Statistics (2014).

[15] Li, Y., Yang, M. and Zhang, Z. Multi-view representation learning: A survey from shallow methods to deep methods. arXiv preprint arXiv:1610.01206 (2016).

[16] Witten, D.M. and Tibshirani, R.J. Extensions of sparse canonical correlation analysis with applications to genomic data. Statistical applications in genetics and molecular biology (2009).

[17] Bach, F.R. and Jordan, M.I. A probabilistic interpretation of canonical correlation analysis (2005).

[18] Archambeau, C., Delannay, N. and Verleysen, M. Robust probabilistic projections. In Proceedings of the 23rd International conference on machine learning (2006).

[19] Wang, C. Variational Bayesian approach to canonical correlation analysis. IEEE Transactions on Neural Networks (2007).

[20] Viinikanoja, J., Klami, A. and Kaski, S. Variational Bayesian mixture of robust CCA models. Machine Learning and Knowledge Discovery in Databases (2010).

[21] De Bie, T. and De Moor, B. On the regularization of canonical correlation analysis. Int. Sympos. ICA and BSS (2003).

[22] Shawe-Taylor, J. and Sun, S. Kernel methods and support vector machines. lecture notes (2009).

[23] Fukumizu, K., Bach, F.R. and Gretton, A. Statistical consistency of kernel canonical correlation analysis. Journal of Machine Learning Research (2007).

[24] Reiter, M., Donner, R., Langs, G. and Bischof, H. 3D and infrared face reconstruction from RGB data using canonical correlation analysis. In Pattern Recognition, (2006).

[25] Zheng, W., Zhou, X., Zou, C. and Zhao, L., 2006. Facial expression recognition using kernel canonical correlation analysis (KCCA). IEEE transactions on neural networks, 17(1), pp.233-238.

[26] Huang, H., He, H., Fan, X. and Zhang, J. Super-resolution of human face image using canonical correlation analysis. Pattern Recognition, 43(7) (2010).

[27] Kim, T.K., Wong, S.F. and Cipolla, R.Tensor canonical correlation analysis for action classification. In Computer Vision and Pattern Recognition (2007).

[28] Sun, T. and Chen, S. Locality preserving CCA with applications to data visualization and pose estimation. Image and Vision Computing (2008).

[29] Yang, W., Yi, D., Lei, Z., Sang, J. and Li, S.Z. 2D–3D face matching using CCA. In Automatic Face & Gesture Recognition (2008).

[30] Dhillon, P., Foster, D.P. and Ungar, L.H. Multi-view learning of word embeddings via cca. In Advances in Neural Information Processing Systems (2011).

[31] Faruqui, M. and Dyer, C. Improving vector space word representations using multilingual correlation. Association for Computational Linguistics (2014).

[32] Blitzer, J. Domain adaptation of natural language processing systems (Doctoral dissertation, University of Pennsylvania) (2008).

[33] Kim, Y.B., Snyder, B. and Sarikaya, R. Part-of-speech Taggers for Low-resource Languages using CCA Features. In EMNLP (2015).

[34] Tripathi, A., Klami, A. and Virpioja, S. Bilingual sentence matching using kernel CCA. In Machine Learning for Signal Processing (MLSP) (2010).

[35] Udupa, R. and Khapra, M.M. Transliteration Equivalence Using Canonical Correlation Analysis. In ECIR (2010).

[36] Baltrušaitis, T., Ahuja, C. and Morency, L.P. Multimodal Machine Learning: A Survey and Taxonomy. arXiv preprint arXiv:1705.09406 (2017).

[37] Mogadala, A. and Rettinger, A. Multi-modal Correlated Centroid Space for Multi-lingual Cross-Modal Retrieval. In ECIR (2015).

[38] Zhu, X., Huang, Z., Shen, H.T. and Zhao, X. Linear cross-modal hashing for efficient multimedia search. In Proceedings of the 21st ACM international conference on Multimedia (2013).

[39] Kettenring, J.R. Canonical analysis of several sets of variables. Biometrika (1971).

[40] Rupnik, J. and Shawe-Taylor, J. Multi-view canonical correlation analysis. In Conference on Data Mining and Data Warehouses (2010).

[41] Shen, C., Sun, M., Tang, M. and Priebe, C.E. Generalized canonical correlation analysis for classification. Journal of Multivariate Analysis (2014).

[42] Tenenhaus, A. and Tenenhaus, M. Regularized generalized canonical correlation analysis. Psychometrika (2011).